Welcome to our Research Group

|
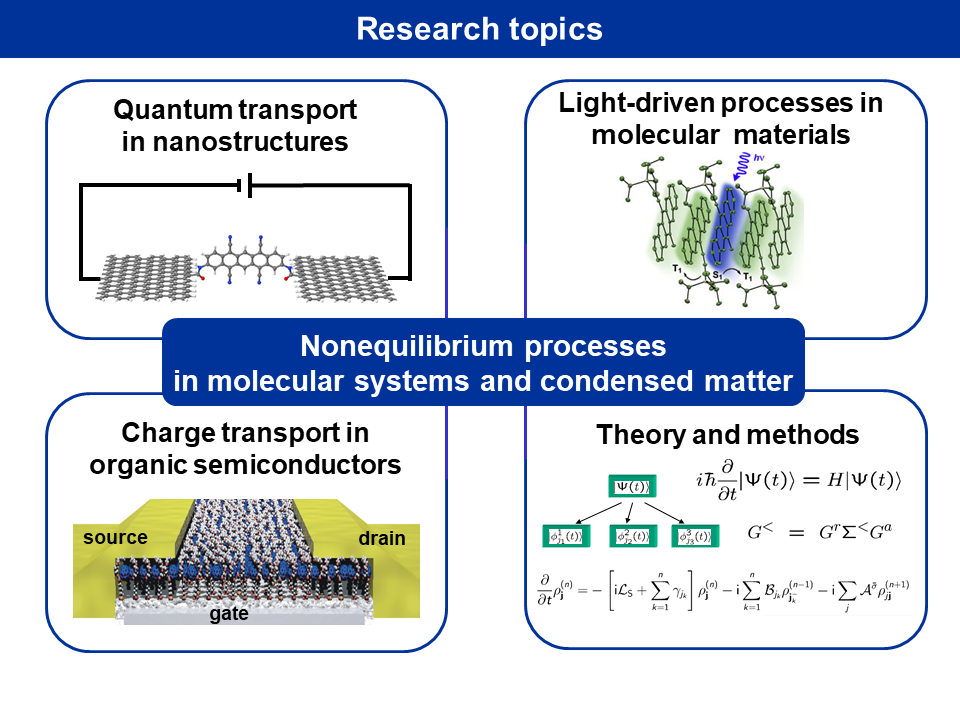
Our research covers a broad range of topics in the fields of theoretical condensed matter and materials physics, chemical physics and nanophysics. The focus is the theory and simulation of nonequilibrium processes in many-body quantum systems, including nanostructures, surfaces, interfaces, and molecular systems. Theoretical and computational methods are being developed and applied to understand fundamental aspects of dynamics and transport in complex quantum systems. Applications include the simulation of charge- and energy transport as well as light-induced processes in the context of nanoscience and energy conversion, often in close collaboration with experimental groups from physics, chemistry, and materials science. |
| |
 |





